Introduction:
Paving and streetmasonry can, at times, seem littered with references to barely-remembered geometric terminology, but most of it is comparatively simple and based around the geometry of circles and right-angled triangles.
Much of that geometry is most easily explained using kerbs as an example, as they are often the closest physical manifestation we have to the geometry created by a designer, specifier or architect. However, the same geometric terms and relationships apply to all aspects of paving, streetmasonry and hardscapes. Just take a look at the work done in preparing a flagstone fan radius, if further proof is needed!
This page sets out to define some of the most commonly encountered terms.
Circle and Arc Definitions
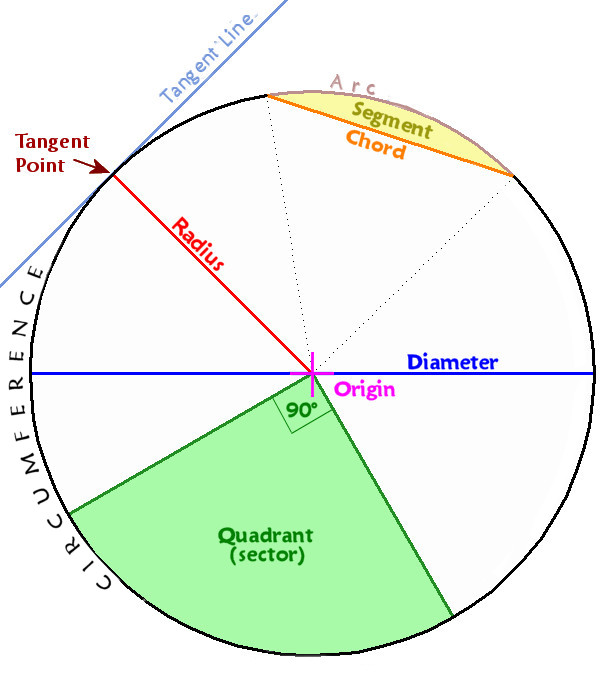
The centre of a circle. The point from which a radius is swung. All points on a circle's outer edge (circumference) are the same distance from the origin.
Radius
This has to be the most commonly used term in streetmasonry, which tends to focus on kerblines of a given radius and fancy set-outs, but it is also used with more simple paving projects.
The radius is the distance from the centre of a circle (the origin) to any point on its outside edge (the circumference)
The plural is sometimes referred to as radii (ray-di-eye)
A physical line following the radius, from the origin out to the circumference, may also be known as a radial

Diameter
The diameter is the span across a full circle, from one side to the other passing through the origin.
Any line touching the circle circumference in two places and passing through the origin MUST be a diameter.
The diameter of a circle is always equal to two radii

Tangent
A line or other geometrical construction (could be another circle, an arc or and ellipse) is said to be a tangent, or is tangential to, when it meets or 'kisses' a circle or arc at only one point.
Tangent Point
The point where a tangent meets or 'kisses' the circle
This term is most commonly used to describe the point on a kerbline where a straight line becomes a curve. The kerbs of the tangent line will be straight units, but once past the tangent point, the kerbs may be radius units or be laid to an arc.

Arc
An arc is any part of the circumference of a circle.
It may be relatively short and shallow, or it could be almost a full circle.
Bends and curves are formed using one or more arcs

Quadrant
A quadrant is the area under an arc that is exactly one-quarter of a full circle.
In classical geometry, the area under an arc is known as a 'sector'. A quadrant is a special type of sector.
The term 'Quadrant' may refer to the arc or to the sector enclosed by two radial lines set at 90°
Single-piece quarter-circle kerbs are often known as "Quadrants" or "Cheeses"

Chord
Whereas a tangent only touches the circumference of a circle or arc at one point, a chord touches at two points.
When such a line passes through the origin, it is a diameter, but any other line touching the same circle or arc at two points is a chord.
Chords can be very useful when it's necessary to determine the radius of an arc from a single kerb or short section of arc...see drawing opposite.
This technique is explained in greater detail on a separate page...
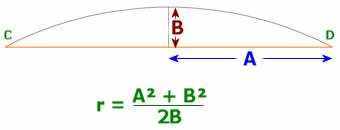
Create a chord, here labelled C - D, and measure its length. Divide by 2 and refer to as "A"
Measure perpendicular distance from arc to mid-point of chord. Refer to as "B"
Add together the square of A plus the square of B
Divide the result by 2B (twice what was measured as a perpendicular)
Segment
As previously described, the area of a circle bounded by an arc and two radii is referred to as a sector. Similarly, the area bounded by an arc and a chord is known as a segment.
Segments aren't widely used in paving and streetmasonry but are included here for completeness.

Circle and Arc Equations
Calculating circumference
The circumference of a circle is calculated using Pi (Π) which can be as a fraction, 22/7, or as a decimal number, roughly 3.142
C = 2 x Π x r
Where
C = circumference
Π = 3.142
r = radius of the circle
So: a circle with a measured radius of, say, 2.4m has a circumference of...
2 x 3.142 x 2.4 = 15.08m
For the length of an arc, the calculated circumference is simply multiplied by the ratio of the angle of the arc over 360°...
arc = 2 x Π x r x (∠ ÷ 360)
Where C = circumference Π = 3.142 r = radius of the circle ∠ = angle of arc
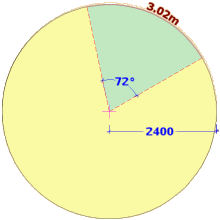
So: in our 2.4m radius circle described above, an arc of 72° has a circumference of...
2 x 3.142 x 2.4 x (72 ÷ 360)
15.08 x 0.2 = 3.02m
Calculating area
Generally speaking, the ability to calculate the area of a circle or arc is more useful to the typical paving contractor than circumference, and once again, the calculation depends on that magic figure, Π
A = Π x r²
Where
A = Area
Π = 3.142
r = radius of the circle
So: the now-familiar circle with a measured radius of 2.4m has an area of...
3.142 x (2.4 x 2.4)
3.142 x 5.76 = 18.1m²
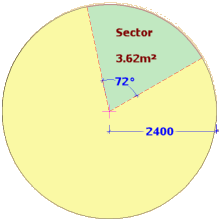
For the area under an arc (more correctly known as a 'sector'), the calculated whole circle area is simply multiplied by the ratio of the angle of the arc over 360°...
A = Π x r²: (∠ ÷ 360)
Where
A = Area of sector
Π = 3.142
r = radius of the circle
∠ = angle of arc
So: in our 2.4m radius circle described above, an arc of 72° has a sector with an area of...
3.142 x (2.4 x 2.4) x (72 ÷ 360)
3.142 x 5.76 x 0.2 = 3.62m²
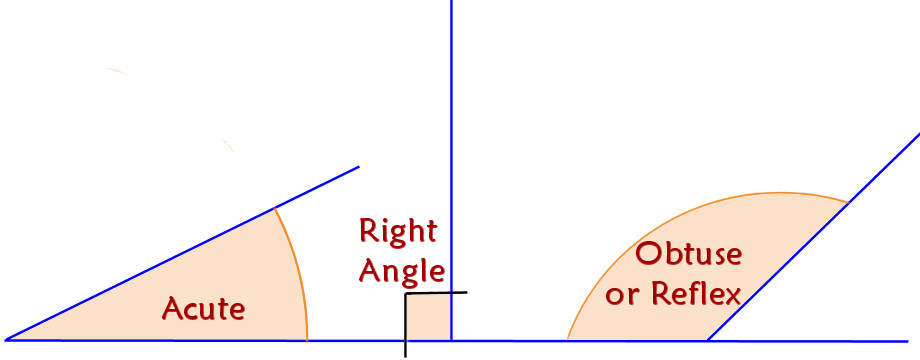
Angles:
There are three basic 'angles' that are discussed when considering the setting-out or measuring-up of paving works:
Acute: - an angle that is LESS than 90°
Right Angle: - an angle that is exactly 90°
Obtuse or Reflex: - an angle that is MORE than 90°